Continuando con la explicación del funcionamiento de la variable dummy, es preciso recurrir a a la siguiente ilustración gráfica:
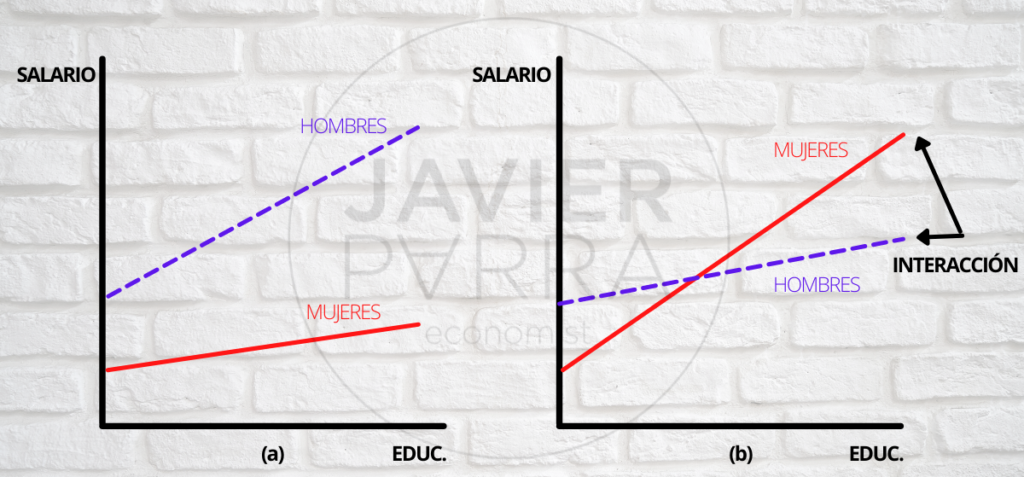
Interacción: La interacción tanto el intercepto como de la pendiente con la variable dummy de la mujer permite modelar ecuaciones salariales completamente independientes para hombres y mujeres.
Hipótesis nula
Ho : δ0 = 0, δ1 = 0, δ2 =0, δ3 = 0
Todos los efectos de interacción son nulos, es decir; se aplican los mismos coeficientes de regresión a hombres y mujeres.
Estimación del modelo no restringido
| pnu = | 1,48 – | 0,353 Mujer + | 0,0011 ppae + | 0,00075 mujer.ppae – | 0,0085 pres – | 0,00055 mujer.pres + | 0,0023 thicu – | 0,00012 mujer. thicu |
| (0,21) | (0,411) | (0,0002) | (0,00039) | (0,0014) | (0,00316) | (0,0009) | (0,00163) |
(0,411), (0,00039), (0,00316) y (0,00163) : Si se comprueba individualmente, no se puede rechazar la hipótesis de que los efectos de la interacción sean nulos.
- pnu = Promedio de notas de la universidad
- ppae = Puntuación de la prueba de aptitud estandarizada
- pres = Percentil de rango de la escuela secundaria
- thicu = Total de horas invertidas en cursos universitarios
Comprobación de las diferencias en las funciones de regresión entre los grupos
1- Modelo no restringido (contiene todo el conjunto de interacciones)
pnu = β0+δ0 mujer+β1 ppae+δ1 mujer.ppae+β2 pres+δ2 mujer.pres+β3 thicu +δ3 mujer. thicu+u
2- Modelo restringido (misma regresión para ambos grupos)
pnu = β0 + β1 ppae + β2 pres + β3 thicu + u
Prueba conjunta con F-estadístico

Forma alternativa de calcular el F-estadístico en el caso dado
- Realizar una regresión separada para los hombres y para las mujeres, el SSR no restringido viene dado por la suma del SSR de estas dos regresiones.
- Ejecutar la regresión para el modelo restringido y almacenar el SSR.
- Si la prueba se calcula de este modo, se denomina «Test de Chow«.
- Importante: La prueba asume una varianza de error constante entre los grupos. Previamente debemos comprobar si esta suposición es cierta. Por lo tanto,










