Los préstamos amortizables mediante renta variable en progresión geométrica muestran equivalencia financiera en el origen:
C0 = A (a1 , q) n| i
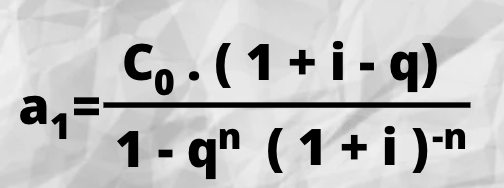
a2 = a1 . q
a3 = a1 . q2
as = a1 . qs-1
A) Cuota de amortización
A1 = a1 – I1 = a1 – C0 . i
As = As . (1 + i) + as . (q – 1)
B) Capital vivo en S
Cs = A (as + 1, q) (n-s)| i = as + 1 . [1-qn-s . (1+i)-(n-s)] / [1 + i – q]
C) Capital amortizado hasta s (Ms)
Ms = C0 – Cs
D) Cuadro de amortización
| S | as | Is | As | Ms | Cs |
|---|---|---|---|---|---|
| 0 | —- | —- | —- | —- | C0 |
| 1 | a1 | I1 = C0 . i | A1 = a1 – I1 | M1 = A1 | C1 = C0 – M1 |
| 2 | a2 = a1 . q | I2 = CI . i | A2 = a2 – I2 | M2 = A1 – A2 | C2 = C0 – M2 |
| … | … | … | … | … | … |
| s | as = a1 . qs-1 | Is = Cs-1 . i | As = as – Is | Ms = A1 + … + As | Cs = C0 – Ms |
| n | an = a1 . qn-1 | In = Cn-1 . i | An = an – In | Mn = C0 | Cn = 0 |
Ejemplo: Calcular el cuadro de amortización de un préstamo de 2.000.000 de u.m. amortizable en 4 años mediante anualidades variables en progresión geométrica de razón 1’04, siendo el tipo de interés el 8% anual.
| S | as | Is | As | Ms | Cs |
|---|---|---|---|---|---|
| 0 | —- | — | — | — | 2.000.000 |
| 1 | 570.934’12 | 160.000 | 410.934’12 | 410.934’12 | 1.589.056’88 |
| 2 | 593.780’84 | 127.124’55 | 466.656’29 | 877.599’41 | 1.122.400’59 |
| 4 | 617.532’07 | 89.792’04 | 527.740’03 | 1.405.339’44 | 594.660’56 |
| 4 | 642.233’35 | 47.572’79 | 594.660’56 | 2.000.000 | 0 |
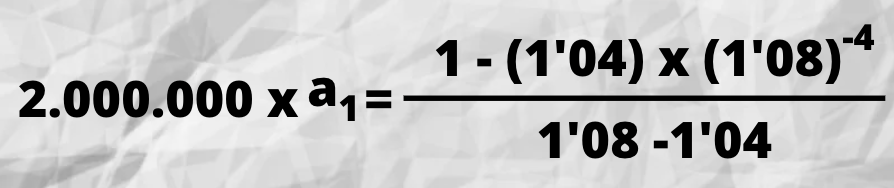
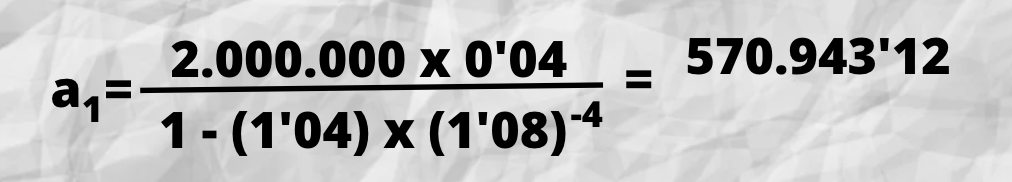
a2 = a1 . q = 570.943’12 x 1’04 = 593.780’84
a3 = a1 . q2 = 593.780’84 x 1’04 = 617.532’07
a4 = a1 . q3 = 617.532’07 x 1’04 = 642.233’35
A1 = a1 – C0 . i = 570.943’12 – 2.000.000 x 0’08 = 410.943’12
A2 = A1 . (1 + i) + a1 . (q – 1) = 410.943’12 x (1’08) + 570.943’12 x (1’04 -1)
A2 = 466.656’29
A3 = A2 . (1+i) + a2 .(q – 1) = 466.656’29 x (1’08) + 593.780’84 x (1’04 -1)
A3 = 527.740’03
A4 =A3 . (1+i) + a3 .(q – 1) = 527.740’03 x (1’08) + 617.532’07 x (1’04 – 1)
A4 = 594.660’56








