Los préstamos amortizables mediante renta variable en progresión aritmética muestran la siguiente equivalencia financiera en el origen:
C0 = A (a1 .h) n| i
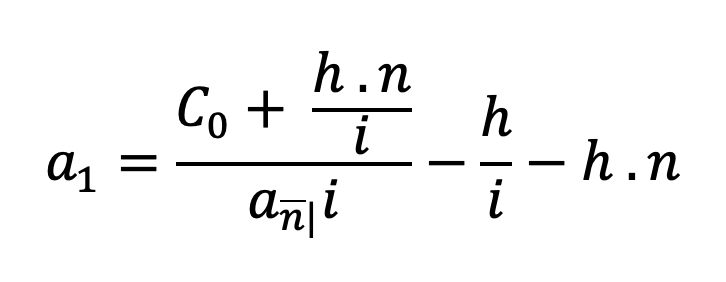
a2 = a1 + h
a3 = a1 + 2h
as = a1 + (s-1) . h
A) Cuota de amortización
A1 = a1 – I1 = a1 – C0 . i
As+1 = As . (1+i) + h
B) Capital vivo en S
Cs = A (as+1, h) n-s| i = [a1 + s . h + h/i + h . (n-s) . a n-s| i – (hh. (n-s) / i)
C) Capital amortizado hasta S (Ms)
Ms = C0 – Cs
D) Cuadro de amortización
| S | as | Is | As | Ms | Cs |
|---|---|---|---|---|---|
| 0 | —- | — | —- | —- | C0 |
| 1 | a1 | I1 = C0 . i | A1 = a1 . I1 | M1 = A1 | C1 = C0 – M1 |
| 2 | a2 = a1 + h | I2 = C1 . i | A2 = a2 . I2 | M2 = A1 + A2 | C2 = C0 – M2 |
| … | … | … | … | … | … |
| s | as = a1 + (s-1) . h | Is = Cs-1 . i | As = as . Is | Ms = A1 +…+ As | Cs = C0 – Ms |
| n | an = a1 + (n-1) . h | In = Cn-1 . i | An = an . In | Mn = C0 | Cn = 0 |
Ejemplo: Establecer el cuadro de amortización de un préstamo de 2.000.000 de u.m. amortizable en 4 años mediante anualidades variables en progresión aritmética de razón 20.000 u.m. siendo el tipo de interés el 5% anual.
| S | as | Is | As | Ms | Cs |
|---|---|---|---|---|---|
| 0 | —- | —- | —- | —- | 2.000.000 |
| 1 | 535.242’59 | 100.000 | 435.242’59 | 435.242’59 | 1.564.757’41 |
| 2 | 535.242’59 | 78.237’88 | 477.004’71 | 912.247’3 | 1.087.752’7 |
| 3 | 535.242’59 | 54.387’65 | 520.854’94 | 1. 433.101’98 | 566.897’76 |
| 4 | 535.242’59 | 28.344’83 | 566.897’76 | 2.000.000 | 0 |
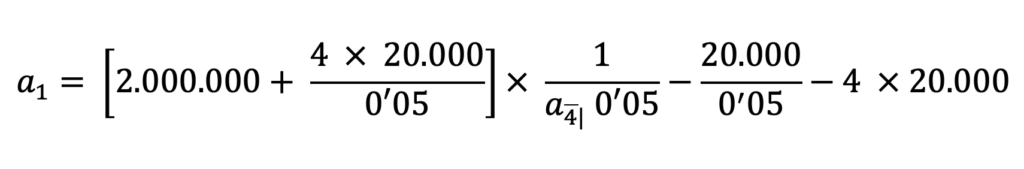
a1 = 3.600.000 x aa’282011832 – 400.000 – 80.000 = 535.242’59 €
a2 = a1 + h = 535.242’59 + 20.000 = 555.242’59
a3 = a2 + h = 535.242’59 + 20.000 = 555.242’59
a4 = a3 + h = 535.242’59 + 20.000 = 555.242’59
A1 = a1 – C0 . i = 535.242’59 – 2.000.000 x 0’05 = 435.242’59
A2 = A1 . (1-i) + h = 435.242’59 x (1’05) + 20.000 = 477.004’71
A3 = A2 . (1-i) + h = 477.004’71 x (1’05) + 20.000 = 520.854’94
A4 = A3 . (1-i) + h = 520.854’94 x (1’05) + 20.000 = 566.897’76








