Una vez visto el préstamo americano, es momento de ahondar en el préstamo alemán, este se caracteriza por:
Términos amortizativos constantes:
a1 = a2 =a3 = … = a
Tantos de interés constantes, pero por anticipado (interés al tirón)
i1 = i2 = i3 = … = i

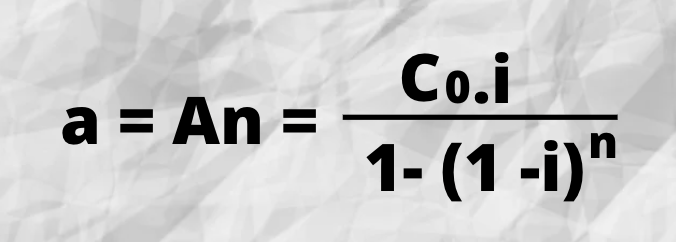
a) Cuota de amortización
As = An . (1-i)n-s
As = As+1 . (1-i)
b) Capital vivo en S
Cs = a . {[1- (1-i)n-s]} / i
c) Total amortizado hasta S (Ms)
Ms = C0 – Cs
d) Cuadro de amortización
| S | as | Is | Aa | Ms | Cs |
|---|---|---|---|---|---|
| 0 | a = C0 . i | I1 = Co . i | — | — | C0 |
| 1 | a = (C0 . i) / [1 – (1-i)n ] | I2 = a – A1 | A1 = An . (1+i)n-I | M1 = A1 | C1 = C0 – M1 |
| s | a | Is+1 = a – As | As = An . (1-i)n-s | Ms = A1 +…+As | Cs = C0 – Ms |
| … | … | … | … | … | … |
| n | a | In+1 = 0 | An = a | Mn = C0 | Cn = 0 |
Ejemplo: Se obtiene un préstamo de 2.000.000 de u.m., amortizable en 4 años al 7% anual por el sistema alemán. Formar el cuadro de amortización.
| S | as | Is | Aa | Ms | Cs |
|---|---|---|---|---|---|
| 0 | 140.000 | 140.000 | — | — | 2.000.000 |
| 1 | 555.670’24 | 108.712’99 | 446.957’25 | 446.957’25 | 1.553.042’75 |
| 2 | 555.670’24 | 75.071’04 | 480.599’2 | 927.556’45 | 1.072.443.’55 |
| 3 | 555.670’24 | 38.896’92 | 516.773’32 | 1.444. 329’77 | 555.670’24 |
| 4 | 555.670’24 | — | 555.670’24 | 2.000.000 | 0 |
a= 2.000.000 / {[1-(1-0’07)4 ] /0’07} = 555.670’24 = a4
a= a4 = 555.670’24
a3 = a4 = (1+i) = 554.670’24 x (1-0’07) = 516.773’32
a2 = a3 = (1-i) = 516.773’32 x (1-0’07) =480.599’2
a1 = a2 = (1-i) =480.599’2 x (1-0’07) =446.957’25






