Para entender la inconsistencia de la TIR es preciso tener presente que hay proyectos de inversión que proporcionan varias tasas de rendimiento e incluso otros que no proporcionan ninguna. Por ejemplo, el proyecto definido como:
-2.000 / 12.500/ -12.500
que es un ejemplo típico de los denominados proyectos de aceleración, que son aquellos en los que una empresa petrolera o minera invierte fondos a fin de acelerar la recuperación de un cierto yacimiento de petróleo o minerales. Dicho proyecto tiene dos tasas de rendimiento: el 25% y el 400%. Por otra parte, el proyecto definido como:
-1.100/ 4.000/ -4.000
carece de tasa de rendimiento real. Este problema se debe a la denominada regla de Descartes que señala que toda ecuación puede tener tantas raíces positivas como cambios de signo existan en la misma. Así pues, los proyectos anteriores tienen dos cambios de signos por lo que podrían tener como máximo dos raíces positivas.
En la figura se muestra la gráfica del VAN del proyecto de aceleración inicial. En ella se aprecia la incongruencia de un proyecto de inversión que posee dos tasas de rendimiento internas de igualmente buenas. No se puede recibir un rendimiento del 25% y que al mismo tiempo también es del 400%; o recibe uno o el otro, pero no ambos. Por eso se dice que la TIR es inconsistente en este tipo de proyectos y que no tiene sentido utilizarla.
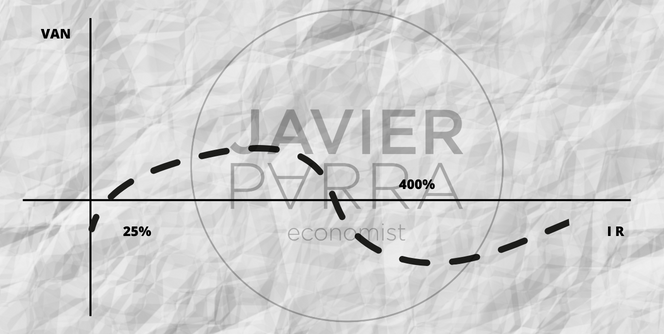
Pero ¿qué ocurre con el VAN? Es evidente que la curva de la figura anterior es la representación del VAN; donde habrá que comprobar que si el tipo de descuento i<25%, su VAN<0; pero que si dicho i>25%, el VAN>0, siempre que i<400%,
Es decir, cuanto mayor sea la tasa de descuento mejor será el proyecto de inversión (al menos hasta un cierto tipo de descuento i=100%), lo que es algo que carece de toda lógica. El VAN también falla en este tipo de inversiones.
Normalmente, es raro encontrarse con este tipo de proyectos de inversión, aunque sí es normal analizar inversiones que tienen más de un cambio de signo entre sus flujos de caja pero que solo tienen una única TIR real positiva. Por ejemplo, cuando una inversión promete ser rentable, sus flujos de caja serán positivos y es factible pensar que tenga que pagar impuestos por los beneficios acecidos a lo largo de los años en los que dicha inversión tiene lugar. Los impuestos sobre la renta se devengan a fin de año pero se pagan aproximadamente con un año de retraso.
Esto quiere decir que los impuestos del año 1 se pagarán en el 2 y, por tanto, figurarán entre los pagos del flujo de caja de dicho año; los impuestos de éste se pagarán en el año 3, etc.; y los impuestos del año n se pagarán en el n+1, siendo el único flujo de caja existente en dicho año, que será obviamente negativo. Así, el último flujo de caja de una inversión empresarial rentable tendrá a ser negativo debido al pago de impuestos. Sin embargo, esto no será mayor problema de cara a la obtención de un única TIR.
En todo caso, el problema es grave pues hemos localizado unas inversiones que aunque «raras» son posibles y que sacan a la luz las limitaciones e inconsistencias de los principales métodos de valoración de inversiones.







