Para hablar de la relación VAN y TIR es preciso comprender que los criterios del VAN y de la TIR suelen coincidir a la hora de determinar qué inversiones son efectuables y cuáles no. Pero en el momento de decidir qué inversión es mejor que otra u otras, ambos métodos no tienen por qué coincidir.
Cuando tenemos que jerarquizar una serie de proyectos de inversión cuyo TIR supera la tasa de rendimiento requerida (i), es decir, que son efectuables, elegiremos primeramente aquel proyecto que proporciona la mayor tasa de rendimiento, en segundo lugar situaremos al que proporciona la segunda mejor tasa de rendimiento y así sucesivamente. Si ahora jerarquizásemos dichos proyectos según el procedimiento analizado en el método VAN, observaríamos cómo no ocupan necesariamente el mismo lugar en ambas listas. Veámoslo mediante un ejemplo.
Las inversiones Alfa y Beta constan de los siguientes flujos de caja (cifra en millones de €):
- ALFA : -100/ 60/ 20/ 70/ 10
- BETA: -45/ 30/ 10/ 50/ 5
Si el tipo de descuento es el 5%, el VAN(alfa)= 44 millones de €, mientras que el VAN(beta)= 40 millones de €, lo que parece indicar que es preferible el proyecto ALFA. Por otra parte, si los jerarquizamos según la tasa de rendimiento, la TIR(alfa)=25,47%, mientras que la TIR(beta)=41,65%. Esto último parece indicar que sería preferible BETA.
Si se procede a graficar, podremos observar que los valores actuales netos de ambos proyectos según el tipo de descuento utilizado para calcularlo. Si dicho tipo de descuento es inferior al 9% el VAN de ALFA es superior al de BETA, mientras que si superase dicho valor ocurriría lo contrario. Por la TIR no hay discusión posible siempre será preferible el proyecto BETA. Al tipo de descuento para el que ambos valores actuales netos coinciden (el 9%) se le denomina tasa de corte FIsher, en honor al economista norteamericano que lo señaló.
El cálculo de la tasa de corte Fisher es muy fácil, puesto que no hay más que igualar los VAN de ambas inversiones y despejar el tipo de descuento que hace posible dicha igualdad.
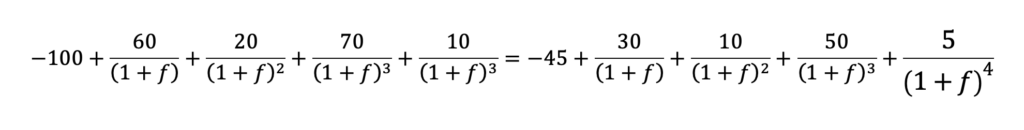
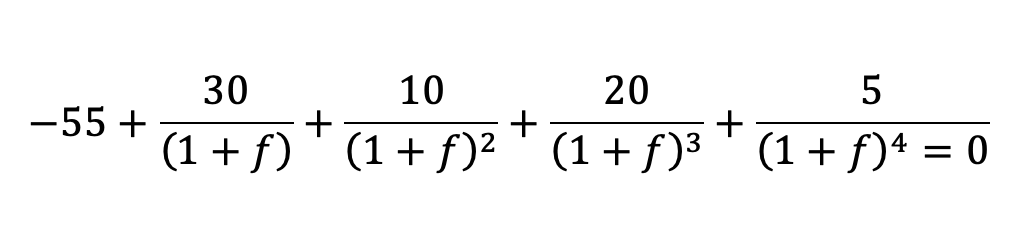
esta ecuación tiene un gran parecido a la clásica expresión matemática de la TIR, de hecho se ha calculado restando término a término cada uno de los quebrados de ambas inversiones por lo que recibe el nombre de inversión diferencia (pero !ojo! no es ninguna inversión real, sino que es la diferencia de dos inversiones ALFA – BETA). Luego la solucionaremos utilizando el mismo procedimiento, esto es, utilizando la calculadora financiera y obtendremos un valor de f aproximadamente igual al 9% (exactamente 8,92%).
Es importante señalar que cuando comparamos las gráficas del VAN de dos inversiones habrá al menos un punto de corte entre ambas (salvo que sean paralelas), pero eso no quiere decir que sea una tasa de corte de Fisher. Esta última sólo existirá cuando el corte se produzca en el primer cuadrante, pues también podría existir una tasa de corte en el segundo cuadrante (por ejemplo para i=0,5%) lo que no tendría sentido económico, o bien, en el cuarto cuadrante (para una i=56%, por ejemplo) que proporcionaría un valor del VAN negativo, lo que tampoco tendría sentido. Lo que sí pueden existir es varias tasas de corte de Fisher en el primer cuadrante.
Así por ejemplo, la inversión Gamma tiene los siguientes flujos de caja: -18.658/ 23.614/ 3.500 y la inversión Delta viene definida por los flujos: -10.000/ 5.000/ 13.500, existirán dos tasas de corte de Fisher para los tipos de descuento del 5,18% y del 9,81%.
La principal razón por la que ambos métodos no coinciden en la jerarquización de los proyectos de inversión, es decir, la razón de la existencia de la tasa de corte Fisher, estriba en que cada método parte del supuesto de que los flujos de caja se reinvierten a un tipo distinto, el VAN los reinvierte al propio tipo de descuento (i), mientras que la TIR lo hace a la tasa de rendimiento.
En resumen, si la tasa de descuento utilizada para calcular los VAN de ambos proyectos de inversión está muy próxima al valor de la tasa de corte de Fisher será necesario tomar una decisión acerca de qué inversión deberá ser seleccionada, para lo cual podríamos utilizar otro criterio de valoración, por ejemplo ls TIR (si ambos proporcionan una ganancia parecida en € será mejor la que tenga un rendimiento mayor). Si la tasa de descuento es inferior a al tasa de corte (i<f) el método VAN preferirá una de las inversiones mientras que la TIR preferirá la otra, lo que nos obligará a elegir uno de los dos sistemas de valoración.








