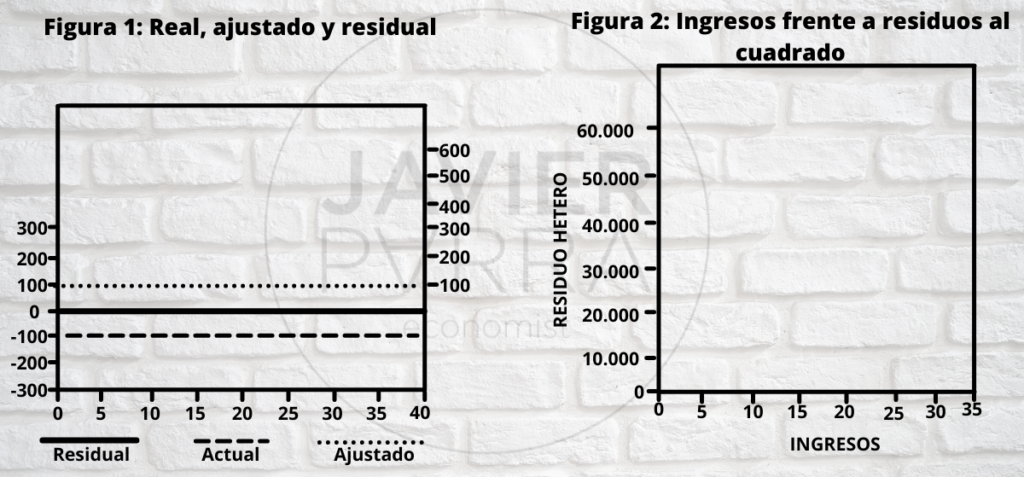
La heterocedasticidad hace una utilización del estimador de mínimos cuadrados de la siguiente forma:
- Inferencia robusta a la heterocedasticidad después de OLS:
- Se han desarrollado fórmulas para los errores estándar de OLS y las estadísticas relacionadas que son robustas a la heterocedasticidad de forma desconocida.
- Todas las fórmulas sólo son válidas en muestras grandes:
- Fórmula para la heteroscedasticidad – error estándar OLS robusto:
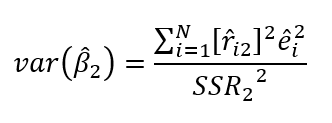
Donde r^i2 es la parte de xi2 que no está correlacionada con xi3 y SRR2 es la suma de los residuos al cuadrado de esta regresión.
De tal forma que:
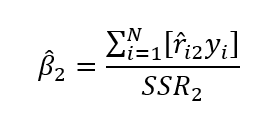
Donde
yi = β1 + β2Xi2 +β3Xi3 +ei
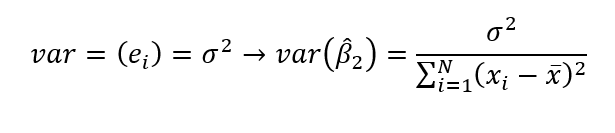
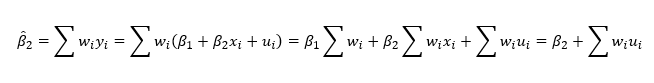
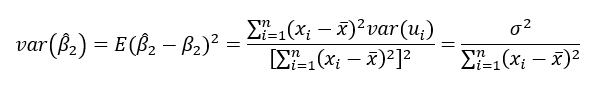
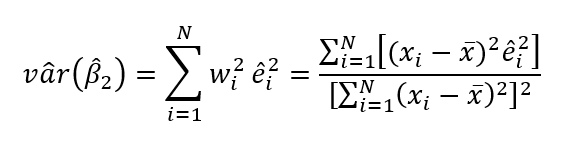
Ahora:
yi = β1 + β2Xi+ei