Para entender el papel que juega el Test Breusch-Pagan en la detección de la heterocedasticidad, es preciso entender que:

y_i = β₁ + β₂X_i2 + …+ u_i  ; var( u_i )=σ²_i  ; [M1]

σ²_i =h(z_i’α) = h(α₀ + α₁z_1i+…+α_pz_pi)

H₀: α₁ = α₂ =…= α_p = 0 ( σ²_i = σ²₀ ∀ i)

H₁: σ²_i = h(z_i’α)

Procedimiento del Test Breusch-Pagan

1- Estimación de M1 por OLS y obtener el residuo OLS.

2- Realizar una regresión del residuo al cuadrado sobre todas las variables explicativas y comprobar si esta regresión tiene poder explicativo.

û²_i= α₀ + α₁z_1i +…+ α_pz_pi +v_i ; R.A-BP

3- Encuentrar el multiplicador estadístico de Lagrange (LM). Los valores altos del estadístico de prueba (= un R-cuadrado alto) conducen al rechazo de la hipótesis nula de que el valor esperado de u² no está relacionado con las variables explicativas.

BP^* =NR² _RA-BP bajo la H₀ X²_p

4- Encuentrar el estadístico F_T1-k,t2-k , (bajo la nula sigue una F donde T1 es el número de observación en la muestra 1 y T2 es el número de observación en la muestra 2)

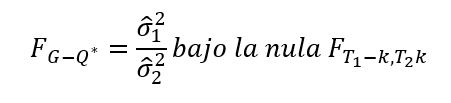
F_G-Q* = 11.11, P – valor= 0,0036

5- Decisión

• Si P(F_{T1 – k, T2 ‘- K}  ≥ F_G-Q *) < α —> Rechazar H₀

• Si P(F_{T1 – k, T2 ‘- K}  ≥ F_G-Q *) >α —> No rechazar H₀

Si se rechaza H₀ significa que hay heterocedasticidad y el OLS no ok.

No olvides compartir

Facebook

Twitter

Linkedin

Whatsapp