Para hablar de colinealidad es necesario entender la regresión lineal, el incumplimiento de los supuestos y sus consecuencias.
Y=Xβ + u
| Supuestos | Fallos |
|---|---|
| S.1. Relación estocástica | |
| S.2. Ausencia de errores de especificación | Variables omitidas/irrelevantes |
| S.3. E(u) =0 | |
| S.4. V(u)=σ2uΣ | Autocorrelación Heterocedasticidad |
| S.5. Linealidad en los parámetros | |
| S.6. X determinística | Regresor estocástico |
| S.7. X1, …, Xk | Dependencia lineal-Multicolinealidad |
| Consecuencias importantes en: | Consistencia Eficiencia |
Ejemplo de colinealidad
- MPG: Millas por galón
- CYL: Número de cilindros
- ENG: Cilindrada del motor en pulgadas cúbicas
- WGT: Peso del vehículo en libras
| Modelo 1 | Modelo 2 |
|---|---|
| MPGi = 42,9 – 3,558 CYLi | MPGi= 44,4 – 2,68 CYLi – 0,0127 RNG – 0,00571 WGTi |
| (se) (0,83) (0,146) | (std) (1,5) (0,413) (0,0083) (0,0071) |
| (p-valor) (0,000) (0,000) | (p-valor) (0,000) (0,517) (0,125) (0,000) |
Identificar la colinealidad
- Examen de la correlación por pares
- Uso de la regresión auxiliar
xi2 = aixi1 + a3xi3 + … + akxik + error
Si el R2 de este modelo es alto, por encima de 0,80, significa que una gran parte de la variación es explicada por la variación de las otras variables explicativas.
Mitigación de la colinealidad
- Obtener más información e incluirla en el análisis.
- Introducir información de la muestra en la de las restricciones de los parámetros
Las consecuencias de la colinealidad: Falta de precisión
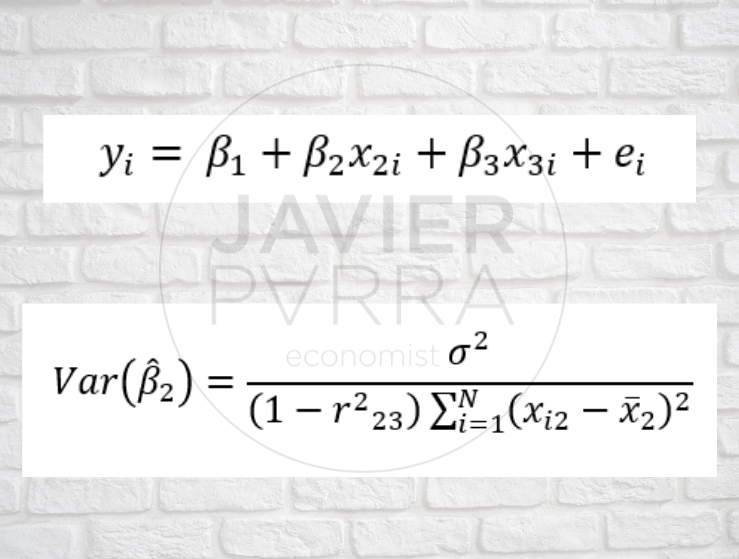
Los efectos de la información imprecisa son:
- Cuando los errores estándar de estimación son grandes, es probable que las pruebas habituales t-pruebas lleven a la conclusión de que las estimaciones de los parámetros no son significativamente diferentes de cero. Este resultado se produce a pesar de los posibles valores altos o f-valores que indican un poder explicativo significativo del modelo en su conjunto.
- Los estimadores pueden ser muy sensibles a la adición o supresión de unas pocas observaciones, o a la supresión de una variable aparentemente insignificante.
- A pesar de las dificultades para aislar los efectos de las variables individuales a partir de una muestra de este tipo, es posible realizar previsiones precisas si la naturaleza de la relación colineal sigue siendo la misma en las nuevas observaciones de la muestra (futura).




