Continuando con el tema de la la detección de heterocedasticidad es importante entender cómo ésta hace uso del test de White,

Test de White para heterocedasticidad

y_i= β₁+β₂X_2i+ β₃X_3i +u_i ; var( u_i )=σ^2_i ; [M1]

• H₀ : σ²₁ =σ²₂=…=σ²_N=σ²_u
• H₁ : σ²₁ ≠σ²_u… y/o σ²_N≠σ²_u

Procedimiento del Test de White

1- Estimar M1 por OLS y obtener el residuo OLS.

2- Regresión de los residuos al cuadrado sobre (i) todas las variables explicativas, (ii) los cuadrados de las variables independientes y (iii) todos los productos cruzados y compruebe si esta regresión tiene poder explicativo.

û²₁= α₀ + α₁x_2i + α₂x_3i + α₃x²₂ + α₄x²_3i + α₅x_2ix_3i + v_i <— Regresión auxiliar -W

3- Multiplicador estadístico de Lagrange (LM). Los valores elevados del estadístico de prueba ( = un R-cuadrado alto) conducen al rechazo de la hipótesis nula de que el valor esperado de u² no está relacionado con las variables explicativas.

W^* = NR² _RA-W bajo la H₀ X²_p, p = # de los parámetros en la regresión auxiliar

4- Decisión:

• Si P(X²_p ≥ BP^*) < α —> Rechazo H₀
• Si P(X²_p ≥ BP^*) > α —> No rechazo H₀

Prueba Breusch-Pagan para la heteroscedasticidad

û²_i = α₀ + α₁z_1i +…+ α_pz_pi + v_i

H₀ : α₁= α₂ = …= α_p =0

Regresión auxiliar: Regresar el residuo cuadrado en todas las variables explicativas y probar si esta regresión tiene poder explicativo.

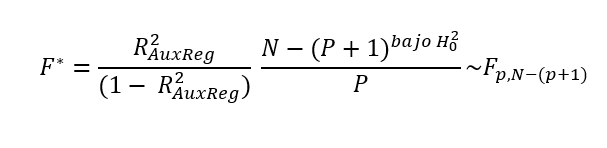
R²_AuxReg: Una estadística de prueba grande (= un R-cuadrado alto) es una prueba contra la hipótesis nula.

Función de heteroscedasticidad desconocida (GLS factible)

y_i = β₁ + β₂X_i2 + …+ β_kX_ik + u_i ; var( u_i )=σ²_i ; [M1]

• σ²_i =h(z’α) = h(α₀ + α₁z_1i+…+α_pz_pi)
• σ²_i = σ² exp(α₀ +α₁z_1i +…+ α_pz_pi)
• u²_i = σ² exp(α₀ α₁z_1i +…+ α_pz_pi) v

σ²_i =h(z’α) = h(α₀ + α₁z_1i+…+α_pz_pi) <— Se asume la forma general de heteroscedasticidad; se utiliza la función exp para garantizar la positividad.

u²_i = σ² exp(α₀ α₁z_1i +…+ α_pz_pi) v <— v: Error multiplicativo (asunción: independiente de las variables explicativas).

—> Log (u²)= α₀ + δ₁x₁ + … + δ_kx_k+e

Log (û²)= α₀ + δ₁x₁ +…+ δ_kx_k + error

—> h_i = exp(α₀ + δ₁x₁ +…+ δ_kx_k)

Valores inversos de la función de heteroscedasticidad estimada como pesos en WLS.

El GLS factible es consistente y asintóticamente más eficiente que el OLS.

Decisión:

• Si P(X²_p ≥ W^*) < α —> Rechazar H₀
• Si P(X²_p ≥ BP^*) > α —> No rechazar H₀

La función de heterocedasticidad debe estimarse mediante GLS factible

y_i = β₁ + β₂X_i2 + …+ β_kX_ik + u_i ; var( u_i )=σ^2₁ ; [M1]

Procedimiento GLS factible

• Estimar M1 por OLS y obtener los residuos OLS.
• Realizar una regresión del log(û²_i) de las variables explicativas y obtenga los valores ajustados.
• Exponenciar los valores ajustados, h_i =exp(Lòg(û²_i)) t estimaciones de la varianza.
• Estimar M1 por WLS utilizando 1/h_i.

No olvides compartir

Facebook

Twitter

Linkedin

Whatsapp