Para esta introducción a la heterocedasticidad debemos partir de hacernos la pregunta ¿Qué es heterocedasticidad y por qué debemos prestarle atención? Para responder consideremos el siguiente resultado de regresión lineal (yi) determinado por una intersección (B1), un conjunto (x2, x3,…, xk), sus coeficientes (β2, β3,…,βj) y un error aleatorio (εi):
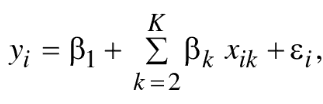
O en notación matricial
y = X β + ε
Donde «y» es un vector de columna Nx1 de los valores del resultado, X es una matriz NxK cuyas columnas son los valores de los predictores. B es un vector de columna de 1xK de los coeficiente, y ε es un vector de columna Nx1 de los valores del término de error.
Uno de los supuestos habituales de mínimos cuadrados ordinarios es que la varianza ε es constante. Var ( ε )=σ2. La heterocedasticidad significa que esta suposición es incorrecta. En cambio, la varianza del error difiere de alguna manera sistemática entre los casos del análisis.
Existen tres situaciones comunes y fácilmente identificables en las que los investigadores deberían apostar fuertemente por el potencial de la heterocedasticidad:
- Al analizar una variable dependiente agregada.
- Al hacer comparaciones entre grupos.
- Cuando la distribución de la variable dependiente esté lejos de ser una distribución simétrica y en forma de campana.
Un ejemplo fácilmente reconocible del ultimo punto es el análisis de una variable dummy dependiente.
Viendo de forma gráfica la heterocedasticidad:

Donde:
- x = ingresos semanales en 100 €
- y= gasto semanal en alimentación en €
yi=83,42 + 10,21xi
ei=yi -83,42 – 10,21xi
var (ei)=h(xi)
Así que para, E(ei)=0, var(ei)= σ2 y cov(ei,ej)=0
La existencia de heterocedasticidad implica:
- El estimador de mínimos cuadrados sigue siendo lineal y no sesgado pero ya no es el mejor. Hay otro estimador con una varianza menor.
- Los errores estándar calculados habitualmente para los estimadores de mínimos cuadrados son incorrectos. Los intervalos de confianza y las pruebas de hipótesis que utilizan estos errores estándar pueden ser engañosos.




