Consideramos dos variables Y y X para las que tenemos algunas observaciones. Nuestro objetivo es estudiar «¿cómo varía Y con el cambio de X?». La forma más sencilla de expresar dicha relación es a través del análisis bivariante, gracias a la regresión lineal bivariante:
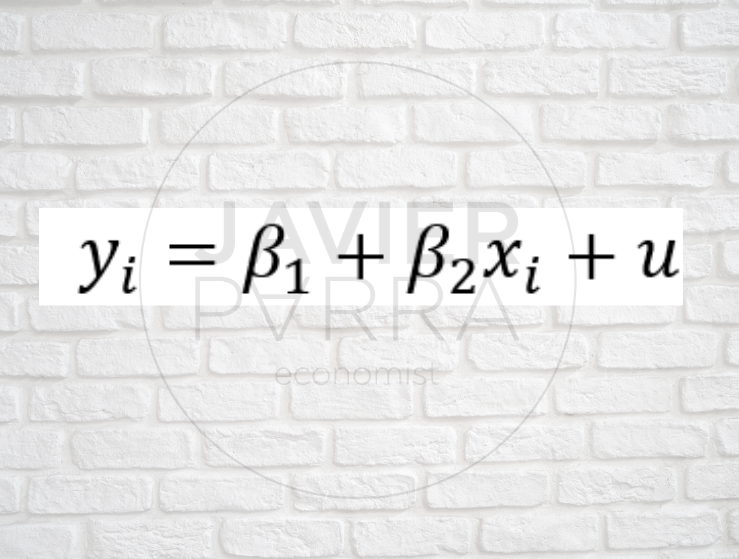
- «Y«: Variable dependiente, variable explicada.
- «X«: Variable independiente, variable explicativa, control, regresor.
- «u«: Término de error o perturbación. Capta el factor distinto de «X» que afecta a «Y». Es inobservable.
- «β2«: Es el parámetro de la pendiente. Es el cambio en E [y[x]] dado un cambio de una unidad en «X», siendo iguales los demás factores relevantes.
- «β1«: Es el parámetro de intecepción.
Por ejemplo:
1- Supongamos que el rendimiento del «tomate» está determinado por el modelo:
rendimientoi= α+βfertilizari+ui
El efecto del fertilizante sobre el rendimiento, en igualdad de condiciones, viene dado por β, Δrendimientoi=βΔfertilizantei. Todos los demás factores, como la igualdad de la tierra, el clima, el riego, etc.
La linealidad del modelo implica que el cambio unitario tiene exactamente el mismo efecto sobre Y, independientemente del nivel inicial de X.
2- Supongamos que la nota final de un estudiante de Econometría se explica por:
EcGPi = α + β medio plazoi + ui => EcGPi =4,11 medio plazoi +ui
El efecto de los parciales en la nota final, en igualdad de condiciones, lo da la β.

Geometría, interpretación y álgebra de las funciones lineales:
yi=β1+β2Xi+ui
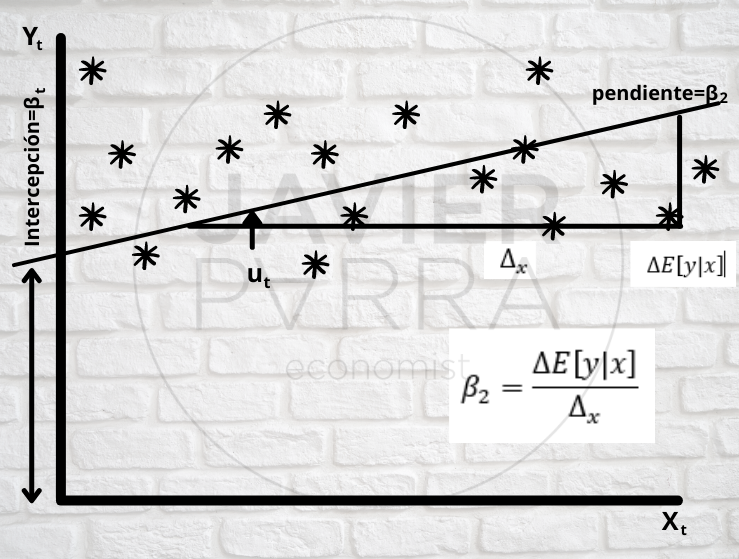
Definición y notacion en el modelo SLR en el análisis bivariante
En el análisis bivariante de regresión simple existe el modelo SLR:
| Lineal | yi=β1+β2Xit+ui |
| Log-Log | Lnyi=β1+β2Lnxit+ui |
| Log-Level | Lnyi=β1+β2Xit+ui |
| Lineal-Log | yi=β1+β2LnXit+ui |
| Cuadrática | yi=β1+β2x2t+β3x3t2+ui |
| Recíproca | yi=β1+(1/xit)β2+ui |
| No lineal | yi=β1+β2X2t+β3X3t+β4X4tXi….ui |
Supuestos del modelo y del parámetro del modelo:
Supuesto 1: lineal en los parámetros
La variable dependiente, se relaciona con la variable independiente, x como:
yi=β1+β2Xi+ui
Las β son parámetros de interés desconocidos y u es un error aleatorio inobservable.
Supuesto 2: Muestreo aleatorio y número de observaciones > número de parámetros
Tenemos una muestra aleatoria de tamaño n {(xi , yi):i=1,2…,n} siguiendo el modelo [1] extraído de la población.
Supuesto 3: Variación de la muestra
Los resultados de la variación de la muestra en x, es decir, {xi , i=1,2,…,n}, no tienen todos el mismo valor.
Supuesto 4: No hay colinealidad perfecta
En la muestra y, por tanto, en la población, ninguna de las variables independientes es constante y no existe una relación lineal exacta entre las variables independientes.
Supuesto 5: Parámetros constantes
En [1] Los parámetros β1, β2, y σ2 (la varianza de u) son números fijos desconocidos con σ>0. Esto significa que, aunque los parámetros del DGP (data generating process) son desconocidos, asumimos que las # observaciones se generan con el mismo valor de los parámetros.
Supuesto 6: El modelo está correctamente especificado
En su ecuación de regresión contiene todos los predictores relevantes, incluidos los términos de transformación e interacción necesarios. Es decir, no hay predictores ausentes, redundantes o extraños en el modelo. Por supuesto, éste es el mejor resultado posible y el que esperamos obtener.
Supuesto 7: u es una media independiente de x
E(ui|xi)=0i para toda i=1, 2, 3…
Supuestos de las perturbaciones (4)
Supuesto 8: Perturbaciones aleatorias, media «condicional» cero
Las perturbaciones aleatorias u1, u2, …, un son variables aleatorias con media cero.
Supuesto 9: Homoscedasticidad
La varianza de las perturbaciones aleatorias u1, u2, …, un existen y son todas iguales.
Var(u2i|xi)=E(u2i|xi)=σ2, para toda i=1,2,3,…
Supuesto 10: No hay correlación
Todos los pares de perturbaciones ui, uj, no están correlacionados:
Cov(ui, uj)=E(ui, uj)=0, para toda i, j=1, …n, i≠j
Supuesto 11: Normalidad
Las perturbaciones u1, u2, …, un se distribuyen conjuntamente de forma normal.
ui~iid N(0,σ2)
Bajo los supuestos 1-11, los valores de yi se distribuyen de forma normal e independiente con media variable y varianza constante, Esto se puede escribir como:
yi~NID(β1+β2xi,σ2) (i=1…,n).





